|
|
 |
|
|
|
|
(Jan 29, 2009)
Andrew B. Watson, Ph.D. - Senior Scientist for Vision Research |
| |
 "If the doors of perception were cleansed every thing would appear to man as it is, infinite. For man has closed himself up, till he sees all things through narrow chinks of his cavern."
- William Blake, The Marriage of Heaven and Hell
As our primary means of gathering information from the world, visual perception is a natural focus of human factors concern. In space and aviation, this is especially true, as humans attempt to navigate through complex and dangerous environments, aided by direct vision and by visual displays. But after four centuries of scientific research, vision is still a complex little understood process. Are there simple principles of vision that we can extract that will be useful in understanding human performance?
One useful characterization of human vision is in terms of a "window of visibility" (Watson et al., 1986). For example, the human eye can sense electromagnetic radiation only within a band of wavelength extending from about 380 to 780 nm. Outside this band, we are blind. This band is thus a relatively narrow window through which we can see. The implications, for the design of displays and visual tasks, are clear.
The concept of a window of visibility can be extended to other dimensions as well. The range of light intensities over which the human eye operates (without damage) is about 13 log units (13 factors of 10, or a range of 1 to 10,000,000,000,000). But the machinery of our visual system cannot handle this large a range at one time. For example, visual neurons can signal effectively only over a range of about 2 log units. In other words, we have a window of sensitivity to light intensity that is only two log units wide. In spite of this limitation, we are able to sense the full 13 log unit range by sliding the window to a range of interest through the process of light adaptation. Essentially the visual system moves the window so that its upper edge is at the highest intensity in view. Here again, this limitation, and our visual system's manner of dealing with it, are critical in the design of visual displays and electronic imaging systems, as well as in understanding the visual challenges of particular lighting environments. One particularly challenging environment may be the surface of the moon, where the absence of an atmosphere creates enormous illumination differences between illuminated and shadowed areas (Kaiser & Ahumada, 2008).
Another critical window of visibility exists in the time domain. As an illustration, most fluorescent lamps produce light whose intensity flickers at 100 to 120 Hz (cycles/sec), yet we do not see the flicker and perceive a steady illumination. This is because the eye cannot sense variations that occur at a frequency higher than about 60 Hz (the "flicker fusion frequency"). Thus we have a window of visibility in the domain of temporal frequency that extends from 0 to 60 Hz. This limit also governs the design of video displays, that are typically refreshed at a rate of 50 or 60 Hz.
Another dimension that can be understood in this way is that of size of spatial detail. It might seem obvious that there are some patterns in a visual image that are too small to see, but it may be less obvious that there are patterns too large to see as well. This counter-intuitive notion may be clarified if we analyze the image not in terms of size, but in terms of spatial frequency. This analysis breaks the image down into its constituent sinusoidal waveforms, just as we analyzed the flickering light, and just as sound can be broken down into component pure tones. In the spatial case, the sinusoids undulate in brightness as they travel across the image (Figure 1). The more rapidly they undulate, the higher the spatial frequency, and the smaller the size of detail. We measure these spatial frequencies in units of cycles/degree, where a degree is an angle subtended at the eye by an object or image (your thumb at arm's length is about 2 degrees wide). Here the upper limit of visibility is about 60 cycles/degree. The lower limit is less sharply defined, but patterns become less visible below 4 cycles/degree, and may very hard to see below 0.1 cycle/degree. So we have another window of visibility in spatial resolution that extends from 0.1 to 60 cycles/degree. These limits are fundamental to a broad range of human factors problems, from the size of typefaces, to the resolution of displays, to the visibility of image compression artifacts, to the distance at which aircraft can be detected.
|
 Figure 1. A sinusoidal grating. Patterns of this kind are used to measure sensitivity to spatial resolution. If you view the pattern from a distance at which it is just covered by your thumb at arm's length, it will have a spatial frequency of about 4 cycles/degree. If you move far enough away, the pattern will change to a uniform gray.
|
What about motion? Our experience tells us that some things move so quickly that they cannot be seen, while others move so slowly that we cannot see them move (the minute hand on a clock). It turns out that these limits can be deduced from two of the windows we have already described: spatial and temporal frequency. This is because the speed of an image component is the product of its spatial and temporal frequencies.
The interaction of spatial and temporal windows is manifest in another important context. You are no doubt aware that movies and television consist of a series of still pictures presented rapidly in sequence - so rapidly that we do not notice the transitions. This illusion is the result of two windows acting in concert: the temporal window and the spatial window. The possible artifact - the physical difference between truly smooth motion and the still sequence - is a set of spatial and temporal frequencies that increase with the detail in the image and the speed of motion, and that decrease with the frame rate (the number of frames per second). By arranging a high enough frame rate, we can ensure that the artifacts are outside of the window of visibility, and the motion will appear smooth (Watson et al., 1986).
Perhaps the most obvious window of visibility is what we call field of view: the cone of angles that we can see with one eye in a fixed position. This is actually a flattened cone, since the horizontal limit (about 150 degrees) is greater than that vertically (about 125 degrees). When the two eyes operate together, the horizontal extent enlarges to about 190 degrees. But as your own experience will show, this window is not equally clear across its extent. Instead, it interacts with the limits of spatial resolution described above. In essence, the size of the spatial resolution window shrinks as we move from the point of fixation (where we are looking) to the periphery. This shrinking is illustrated in Figure 2, which shows relative acuity as a function of degrees from fixation. Fine detail can only be seen in the center, at the margins everything is blurred. For example, the window within which acuity is at least half its maximum is only 3 degrees in diameter! To compensate for this limitation, of course, our eyes move, bringing objects of interest to the high-resolution center of the field of view.
|
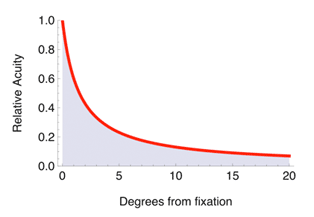
Figure 2. Relative size of the window of spatial resolution as a function of degrees of angle from the point of fixation. At 20 degrees, the window has shrunk by a factor of 10, so that the upper limit would shift from 60 cycles/degree to 6 cycles/degree. Visual acuity would change by a comparable amount.
|
In fact, all of the windows described here interact to some extent, so that the global window that is their combination cannot be so easily described. But to a first approximation, these windows form a powerful description of the "narrow chinks," in Blake's words, though which we see. Knowing these limits is the first step in understanding the human factors of vision.
On a final note, was Blake right? Would we see better if we had no limits? Are the limits we observe failures of biological engineering? Probably not. The eye and brain have evolved to separate signal from noise. The signals - significant objects and events in our environment to which we have the capacity to respond - are embedded in an ocean of noise - insignificant variations or constancies in light over the dimensions of space, time, and wavelength. The windows of visibility are open to the signals, but closed, we hope, to the noise.
|
| Dimensions |
Limits |
Unit |
| Wavelength |
380-780 |
nm |
| Spatial Resolution |
0-60 |
cycles/degree |
| Temporal Resolution |
0-60 |
Hz |
| Field of View |
190 Horizontal
125 Vertical |
degrees |
| Luminance |
100 |
max/min |
Table 1. A summary of important limits to human vision
References and Further Reading
- Boff, K., Kaufman, L., & Thomas, J. (Eds.). (1986). Handbook of Perception and Human Performance. New York: Wiley.
- Kaiser, M. K., & Ahumada, A. J., Jr. (2008, June, 2008). Perceptual challenges of lunar operations. Paper presented at the SAE International, San Francisco, CA, USA, http://vision.arc.nasa.gov/personnel/al/papers/08ices/KaiserAhumada08ICES.pdf ( Download Adobe Acrobat Reader)
- Watson, A. B., Ahumada, A. J., Jr., & Farrell, J. (1986). Window of visibility: psychophysical theory of fidelity in time-sampled visual motion displays. Journal of the Optical Society of America, 3(3), 300-307, http://www.opticsinfobase.org/viewmedia.cfm?uri=josaa-3-3-300&seq=0.
Useful Links
http://vision.arc.nasa.gov/publications.php
|
|
|
|
